7 Intro to Game Theory
Some of the decisions that we make in daily life are done with incomplete information. For example, when you decide to go to a restaurant, you do not know exactly how long you will have to wait for a table, or how good the food will be. The restaurant manager must also decide how to staff the restaurant even though demand is unpredictable. In such situations, you have to make decisions based on what you know and what you think others will do. Game theory allows us to mathematically model situations with incomplete information in order to make the best possible decisions.
7.1 What is Game Theory?
Game theory is a branch of mathematics that studies how people (often called players) make decisions in situations where they have to consider the decisions of others. It is used in a wide range of fields, including economics, political science, biology, and computer science. Game theory is used to model situations where the outcome of a decision depends on the decisions of others.
7.2 Split or Steal?
Watch the following video that we will use to introduce the concept of game theory:
Video summary: Steve and Tracy are playing a game show where they have the chance to win a large sum of money. They have two options: they can either “split” the money, in which case they each get half of the total, or they can “steal” the money, in which case the player who steals gets all of the money, and the player who splits gets nothing.
A Payoff Matrix is a table that shows the possible outcomes of a game. Each player’s payoff is shown in the matrix based on the decisions made by all players. A payoff matrix is one of the ways to represent a game in game theory. Below is the payoff matrix for the “Split or Steal” game:
| Steve splits | Steve steals | |
|---|---|---|
| Tracy splits | Tracy $20K, Steve $20K | Tracy $0, Steve $40K |
| Tracy steals | Tracy $40, Steve $0 | Tracy $0, Steve $0 |
A two-person game is a game in which there are two players who make decisions that affect each other. The “Split or Steal” game is a two-person game. Tracy can choose to split or steal, and Steve can choose to split or steal.
The term strategy in game theory refers to each player’s possible moves. In the above game, both Tracy and Steve have identical strategies (i.e., split and steal”). The payoff is at the intersection of the row (Tracy’s strategies) and the column (Steve’s strategies) chosen by each players. If there are \(m\) strategies for the first player and \(n\) strategies for the second player, then the payoff matrix will be an \(m \times n\) matrix.
A zero-sum game is a game in which if one player wins, the other loses by the same amount. The “split or steal” game described above is not a zero-sum game. More on this later.
7.3 Payoff Matrix
We are going to consider a “simpler” game in order to develop the concept of a payoff matrix even further:
In a penalty shoot out game, there are two players, the kicker and the goalie. The kicker can kick left, right, or straight (center) while the goalie can dive left, right, or stay at the center. If the kicker scores, the goalie pays $10. Otherwise, the kicker pays the goalie $10. We are going to assume that a goal is scored only if the direction of the kick and the goalie’s dive are not the same. For example, a right kick and a left dive result in a goal, in which case the goalie pays $10 to the kicker. The following is the payoff matrix for the penalty shoot out game:
| Dive Left | Dive Center | Dive Right | |
|---|---|---|---|
| Kick Left | 0, 10 | 10, 0 | 10, 0 |
| Kick Center | 10, 0 | 0, 10 | 10, 0 |
| Kick Right | 10, 0 | 10, 0 | 0, 10 |
Things to note:
- The rows represent the kicker’s strategies while the columns represent the goalie’s strategies. This is a \(3\times3\) (read as “three by three”) matrix because there are three strategies for each player.
- The first number in each cell represents the payoff to the kicker, while the second number represents the payoff to the goalie. For example, if the kicker kicks left and the goalie dives left, the kicker gets 0 and the goalie gets 10 (from the kicker).
- The above game is a two-person zero-sum game because the sum of the payoffs to the kicker and the goalie is always zero. This is because the money is transferred from one player (the loser) to another (the winner). No money comes from outside).
7.3.1 Simplified Notation
Although the table above representing the payoffs is fairly easy to grasp, it is often better to represent the information in a manner that shows a single number for each “cell” such that a negative number represents a loss while a positive number represents a gain. As a standard, we use rows as the stand point such that the entry \((10,0)\) is written as \(10\) because the kicker gains $10. Similarly, the entry \(0,10)\) is written as \(-10\) because the kicker loses $10. Furthermore, we can now drop the column and row labels. Note that all this is based on the perspective of the kicker (the rows). The following is the simplified payoff matrix for the penalty shoot out game:
\[\begin{equation} \left[ \begin{array}{ccc} -10 & \phantom{-}10 & \phantom{-}10 \\ \phantom{-}10 & -10 & \phantom{-}10 \\ \phantom{-}10 & \phantom{-}10 & -10 \\ \end{array} \right] \end{equation}\]7.3.2 Dominated Strategies
In the penalty shoot out game described above, if the kicker deploys the first strategy (i.e., kick left), then, the only way he can get a $10-dollar payoff is if the goalie dives right or center. For the kicker, the second and third strategies (center and right kicks) are just as good as the first. A similar argument can be made for the goalie.
A strategy is said to be dominated if there is another strategy that always gives a higher payoff, regardless of the other player’s strategy. In the penalty shootout game above, there is no dominated strategy for either player.
Now, suppose there are certain left kicks (maybe left top corner) for which the kicker will always score even if the goalie dives left. In this case, the payoff matrix will be as follows:
\[\begin{equation} \left[ \begin{array}{ccc} 10 & \phantom{-}10 & \phantom{-}10 \\ 10 & -10 & \phantom{-}10 \\ 10 & \phantom{-}10 & -10 \\ \end{array} \right] \end{equation}\]In this case, if the kicker uses the first strategy (left kick), he will always get a $10 payoff regardless of what strategy the goalie deploys. This is the only strategy that would guarantee a $ 10 payoff to the kicker. We call such a strategy a dominant strategy because it always gives the highest payoff, regardless of the other player’s strategy. For the kicker, the other two strategies are dominated strategies. These are “row 2” and “row 3” in the payoff matrix above.
A given row (say row A) for the first player dominates another row (say row B) if every entry in row A is larger than the corresponding entry in row B. In this case, we call row B a dominated strategy.
For the second player (columns), a given column is dominant if every entry is smaller than the corresponding entry in another column.
Either player can have dominated strategies. Make sure to keep a track of the strategies that are dominated and the ones that are dominant. Since dominated strategies are never the best choice, we often eliminate them from the game.
Example 1:
For each of the following payoff matrices, describe the payoffs for each player then find any dominated strategies. Also, write down the final game by removing the dominated strategies.
Solution:
- This is a two-player \(2\times4\) game. The first player has two strategies while the second player has four strategies. The entry at the intersection of the second row and the second column represents a payoff of one unit to the first player. This is the only positive entry in the payoff matrix. All other entries (negatives) represent payoffs to the second player. Column 2 is a dominated strategy since every entry in column 3 is smaller than every entry in column 2. Similar, column 1 dominates column 2. We can eliminate this strategy (column 2) from the game. The final game is as follows:
- This is a two-player \(3\times2\) game. The first player has three strategies while the second player has two. The zero entry means that there is no payoff for either player when the first player uses the second strategy and the second uses the first.
Each entry in row 3 is larger than the corresponding entry in row 1. This means that the first row is a dominated strategy. We can eliminate this strategy from the game. The final game is as follows:
\[\begin{equation} \left[ \begin{array}{cc} 5 & 3 \\ 0 & 9 \\ \end{array} \right] \end{equation}\]7.4 Strictly Determined Games
Consider the following payoff matrix for a two-player game:
\[\begin{equation} \left[ \begin{array}{ccc} -8 & -9 & \phantom{-}8\\ \phantom{-}2 & \phantom{-}5 & \phantom{-}6 \\ -1& \phantom{-}7 & -2 \end{array} \right] \end{equation}\]Recall that positive numbers in the matrix mean payoffs to the first player (the rows player) while negative numbers mean payoffs to the second player (the columns player). For example, if the first player uses the first strategy (row 1) and the second uses the second strategy (column 2), the first player pays $9 to the second player. This round of play can be represented as \((1,2)\). If instead the second player uses the third strategy, the first player gets $8 from the second player.
In game theory, the goal is to find the most profitable strategy for each player, i.,e., the strategy that maximizes the payoff or minimizes the payoff to the opponent. Here are important terminologies that we will use in the discussion of the game above:
An optimum Strategy for any given player in a game is the strategy that results in the most payoff to the player or, in some cases, the least payoff to the opponent.
The value of the game is the payoff amount resulting from both players using their optimum strategies.
A fair game is a game with a value of zero. This means that no player takes a loss.
In order to determine the value of the game, we will need to look at the possibilities that player 2 has when player one chooses strategy 1, 2, and 3. This can be best summarized in the table below:
| If Player 1 chooses |
Player B would choose |
With a Payoff of |
|---|---|---|
| Row 1 | Column 2 | $9 to player 2 |
| Row 2 | Column 1 | $2 to player 1 |
| Row 3 | Column 3 | $2 to player 2 |
From the table above, we can see that the best strategy (optimum strategy) for player 1 is to choose row 2. This is because player 1 is guaranteed a minimum of $2 every time he chooses row 2. Note that player 1 can get more if player 2 messes up by, say, choosing column 3.
Similarly, player 2’s best strategy is to choose column 1 because this minimizes the amount that he has to pay to player 1. The value of the game is the payoff at the intersection of row 2 and column 1 (i.e., $2). The is not fair game because the value of the game is not zero.
Notice that the entry 2 in the payoff matrix is the smallest entry in its row and the largest in its column.
A saddle point in a payoff matrix is the smallest in its row and the largest in its column.
A strictly determined game is a game containing a saddle point. The value of the game is the payoff at the saddle point.
Example 2:
Consider the following payoff matrix:
\[\begin{equation} \left[ \begin{array}{ccc} -3 & -2 & \phantom{-}6\\ \phantom{-}2 & \phantom{-}0 & \phantom{-}2 \\ \phantom{-}5 & -2 & -4 \end{array} \right] \end{equation}\]What would be the payoff for the strategy (2,3)? Note that here, player 1 (rows) plays strategy 2 while player 2 (columns) plays strategy 3.
Find the optimum strategy for each player. Recall that player 1 is the row player while player 2 is the column player.
Is the game strictly determined? Why or why not?
What is the value of the game?
Is the game fair? Why or why not?
Solution:
The payoff for the strategy (2,3) is $2 to player 1. This is because player 1 (row 2) pays $2 to player 2 (column 3).
To find the optimum strategies for each player, we can start by making a payoff summary table as follows:
| If Player 1 chooses |
Player B would choose |
With a Payoff of |
|---|---|---|
| Row 1 | Column 1 | $3 to player 2 |
| Row 2 | Column 2 | $0 to player 1 |
| Row 3 | Column 3 | $4 to player 2 |
Based on the table, the optimum strategy for player 1 is to choose row 2. The optimum strategy for player 2 (assuming player 1 chooses row 2) is to choose column 2. Thus, the optimum strategy is (2,2).
To determine whether the game is strictly determined we find the saddle point. The smallest entry in each row is -3, 0, and -4 respectively from row 1 to 3. The largest among these is 0. Next, the largest entry in each column is 5, 0, and 6 respectively from column 1 to 3. The smallest among these is 0.
Therefore, the saddle point is 0 (recall that saddle point is the largest in its column and the smallest in its row). Since the game has a saddle point, it is a strictly determined game.The value of the game is the payoff at the saddle point. This is $0.
The is a fair game because the value of the game is zero. This means that no player takes a loss.
Example 3:
Determine whether the following game is strictly determined or not. If it is, find the strategy producing the saddle point then find the value of the game:
\[\begin{equation} \left[ \begin{array}{ccc} 4 & \phantom{-}7 & -1\\ 9 & -2 & \phantom{-}6 \\ \end{array} \right] \end{equation}\]Solution:
We can start by underlining the smallest entry in each row as follows:
\[\begin{equation} \left[ \begin{array}{ccc} 4 & \phantom{-}7 & \underline{-1}\\ 9 & \underline{-2} & \phantom{-}6 \\ \end{array} \right] \end{equation}\]Next, we can bold the largest entry in each column:
\[\begin{equation} \left[ \begin{array}{ccc} 4 & \phantom{-}\textbf{7} & \underline{-1}\\ \textbf{9} & \underline{-2} & \phantom{-}\textbf{6} \\ \end{array} \right] \end{equation}\]Now, since there is no entry that is both underlined and boldfaced. Therefore, the game has not saddle point and is not strictly determined.
Many students find this approach of underlining and boldfacing easier to use. I encourage you to try this approach on example 2 above.
Example 4:
A soft drinks company has developed a new drink that it believes will increase their market share and sales volume. The company has a decision to make: advertise the new drink aggressively, moderately, or not to advertise at all. Customers may or may not like the new drink. If the company advertises the drink aggressively, sales will increase by $60,000 if customers like the drink. Otherwise, sales will decrease by $45,000. If the company advertises moderately, sales will increase by $40,000 if customers like the drink and decrease by $35,000 if they don’t. If the company decides to not advertise the drink, sales will decrease by $50,000 if customers like the drink and by only $10,000 if they don’t.
- Create a payoff matrix to model the above scenario. Use Decision (Aggressive Ads., Moderate Ads., No Ads.) as the rows and Customer Attitude (Like or Don’t Like) as the Columns.
- The company believes that there is a 45% chance that customers will like the new drink. Use this information to find the expected profits under each strategy and determine the best strategy.
- Are there any dominated strategies? Find them.
- Find a saddle point if one exists. Is the game strictly determined?
Solution:
The payoff matrix is shown below. The rows represent company decision while the columns represent customer attitude.
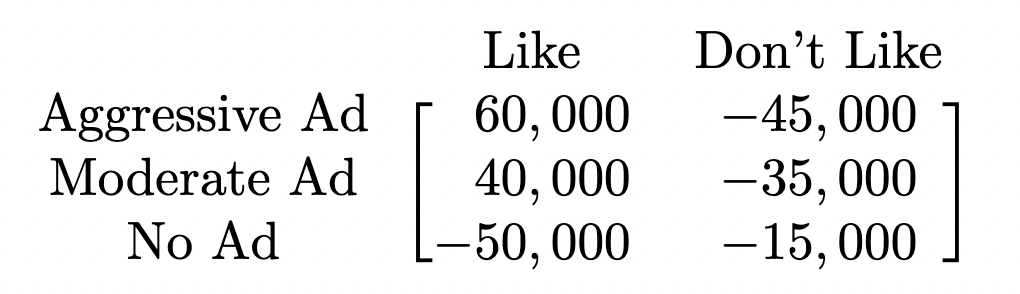
The expected profits under each strategy are as follows:
- Aggressive Ads.: \((60,000 \times 0.45) + (-45,000 \times 0.55) = \$7,500\)
- Moderate Ads.: \((40,000 \times 0.45) + (-35,000 \times 0.55) = \$2,750\)
- No Ads.: \((-50,000 \times 0.45) + (-10,000 \times 0.55) = -\$27,500\)
The best strategy is to advertise the drink aggressively.
For dominated strategies,
- Recall that for player 1 (rows), a astrategy is dominant of all entries in the row are larger than the corresponding entries in another row. For player 2 (columns), a strategy is dominant if all entries are smaller than the corresponding entries in another column. Since non of the strategies satisfy this condition, there are no dominated strategies.
To find a saddle point, we can underline the smallest entry in each row and boldface the largest entry in each column:
\[\begin{equation} \left[ \begin{array}{cc} \phantom{-}\textbf{60} & -\underline{45} \\ \phantom{-}40 & -\underline{35} \\ -\underline{50} & -\textbf{10} \end{array} \right] \end{equation}\]Since there is no entry that is both underlined and boldfaced, there is no saddle point, and hence the game is not strictly determined.
7.5 Exercises
For each of the following payoff matrices, state the number of players in the game, the number of strategies for each player, and describe the payoffs for each player:
\[\begin{equation} \left[ \begin{array}{ccc} -8 & -6 & -9\\ -1 & -8 & \phantom{-}12 \\ \end{array} \right] \end{equation}\]
- \[\begin{equation} \left[ \begin{array}{cccc} -9 & -7 & -9&\phantom{-}7\\ -1 & \phantom{-}0 &\phantom{-}8 & \phantom{-}3\\ \phantom{-}5 & \phantom{-}4 & -3 & -2 \end{array} \right] \end{equation}\]
For each matrix in question 1, find the payoffs when the following strategies are played:
(1,2)
(2,3)
(3,4); this applies only for (b)
(1,3)
(2,2)
For each of the following payoff matrices, find any dominated strategies and write down the final game by removing the dominated strategies:
\[\begin{equation} \left[ \begin{array}{cc} \phantom{-}4 & \phantom{-}7 \\ \phantom{-}2 & \phantom{-}5 \\ \phantom{-}5 & -1 \\ -3 & -1 \end{array} \right] \end{equation}\]
- \[\begin{equation} \left[ \begin{array}{ccc} 9 & \phantom{-}8 \\ 0 & -3 \\ 6 & \phantom{-}11 \\ \end{array} \right] \end{equation}\]
For each of the following payoff matrices, find the optimum strategy for each player, determine whether the game is strictly determined or not, and find the value of the game:
\[\begin{equation} \left[ \begin{array}{cc} 8 & \phantom{-}6 \\ 12 & -4 \\ \end{array} \right] \end{equation}\]
\[\begin{equation} \left[ \begin{array}{cccc} -4 & 2 & -3 & -7 \\ \phantom{-}4 & 3 & \phantom{-}5 & -9 \\ \end{array} \right] \end{equation}\]
- \[\begin{equation} \left[ \begin{array}{ccccc} 1 & \phantom{-}4 & -3 & \phantom{-}1&-1 \\ 2 & \phantom{-}5 & \phantom {-}0 & \phantom {-}4&\phantom {-}10 \\ 1 & -3 & \phantom{-}2 & \phantom {-}5&\phantom{-}2 \\ \end{array} \right] \end{equation}\]
Sweet Melodies Band is planning to hold a concert and all tickets are already sold out. Since the weather is unpredictable, the band must decide in advance on three options: to hold the concert indoors, outdoors, or set up seats both indoors and outdoors. If the show is held outdoors, the band will make a profit of $23,000 when there is no rain and a loss of $17,000 if it rains. If the show is held indoors, the band will make a $16,000 profit whether it rains or not. If they decide to set up some seats indoors and some outdoors, the band will make $13,000 if it rains and $21,000 if it doesn’t rain.
Create a payoff matrix to model this scenario. Be sure to label the matrix accordingly. Use “Band Decision” as player 1 (i.e., rows) and “Weather” as player 2 (i.e., columns).
Find the optimum strategy for the band.
Is the game strictly determined? Why or why not?
What is the value of the game?
Suppose the weather forecast shows that there is a 60% chance of rain. What would be the best decision for the band (i.e., what strategy would maximize the profit)?
Two armies, A and B are involved in a war. Each army has available three different strategies, with payoffs as shown in the payoff matrix below. These payoffs represent square miles of land, with positive numbers representing gains by A (the rows army). Find the strategy producing the saddle point and the value of the game. (Adapted from Finite Mathematics by Lial et. al.)
\[\begin{equation} \left[ \begin{array}{ccc} -8 & -10 & \phantom{-}4\\ \phantom{-}0 & -12 & \phantom{-}6 \\ \phantom{-}3 & -7 & \phantom{-}8 \end{array} \right] \end{equation}\]
